como para el otro tipo de ecuacion primero debemos encontrar ciertas variables tales como a,b y c conociendo el centro el foco y un vertice ( lo que se conoce no aplica para todas los ejercicios )
ahora un ejemplo
- centro (1,1); foco ( 4,1); vertice (6,1)
Para el siguiente paso del rompecabezas hallamos a es decir la distancia del centro al vertice, para conocer la formula investigue el inicio del blog , o el de linea recta.
Para continuar lo que se hizo fue encontrar b con el teorema de pitagoras ya conociendo a y ,
ya que se tienen todos los valores necesarios será sencillo expresar la ecuacion.
Ejercicios de aplicacion
- centro (-3,2); foco (4,2); vertice (7,2)
- centro (2,4); foco (-1,4); vertice (-3,4)
- centro (-5,-3); foco (0,-3); vertice (1,-3)
Parte - 1
Parte - 2

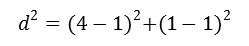








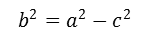





No hay comentarios:
Publicar un comentario