Con esta ecuacion determinamos el eje mayor y el eje menor mientras conoscamos la ecuacion para encontrar a, lo unico que se debe hacer es sacarle la raiz cuadrada lo mismo para encontrar b en la ecuacion conocemos ambas variables elevadas al cuadrado un simple proceso de despeje y es muy facil encontrar la respuesta.
Recordemos que c será igual a la distancia entre el foco y el centro de la elipse , es decir que si no tenemos c y tenemos un foco y el centro sera igualmente rapido hallar la variable.
Cuando se conocen dos variables la ecuacion a recurrir sera el famoso teorema de pitagoras,
ya que cuando no se conosca una variable sera sencillo de encontrarla con este metodo
Ahora un ejemplo de la ecuacion de la elipse con el centro en el origen
encuentre la ecuacion de la elipse con el centro en (0,0) ; foco en (3,0); vertice en (5,0)
Esta es la grafica de la elipse mencionada en el ejemplo, sin embargo en la grafica aparece el foco primo plasmado como B, para desarrollar el problema despreciaremos este dato.
asi que para encontrar la ecuacion lo que debemos hacer es sacar la diferencia entre el vertice y el centro
Ya que sacamos la distancia entre el origen y el vertice podemos deducir que d sera igual a a tambien sabemos que a elevado al cuadrado sera 25, y ya tenemos la primera variable encontrada ahora encontraremos b, pero para encontrar b primero debemos encontrar c lo cual conocemos como la distancia del centro al foco.
En esta ocasion d será igual a c y al final ya que conocemos c podremos encontrar b
ahora podremos decir que la ecuacion de la elipse es
Ejercicios de aplicacion
- centro (0,0); foco (1,0); vertice (6,0)
- centro (0,0); foco (0,-3); vertice (0,4)
- centro (0,0); foco (2,0); vertice (4,0)
- centro (0,0); foco (-5,0); vertice (6,0)
- centro (0,0); foco (-4,0); vertice (8,0)
Ahora el video de la demostracion
preparense para sufrir al estilo analitico.
Esta es la segunda parte







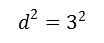










No hay comentarios:
Publicar un comentario