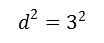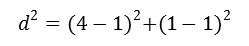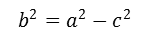La distancia entre uno de sus puntos y el centro se le conoce como radio y la recta entre dos puntos que pasa por el centro se le conoce como diametro, esto significa que la longitud del diametro de una circunferencia es el radio multiplicado por dos.
La circunferencia posee varios puntos, rectas y segmentos ademas del centro, diametro y radio tales como:
Cuerda: es el segmento que une dos puntos de una circunferencia (el diametro es la cuerda de mayor longitud).
Recta secante: es la recta que corta la circunferencia en dos puntos .
Recta tangente: es la recta que toca la circunferencia en un solo punto.
Punto de tangencia: es el punto de interseccion de la recta tangente con la circunferencia.
Arco: es el segmento curvilineo de puntos pertenecientes a la circunferencia
Aunque son parte importante de la circunferencia no serán vistas con detalle en este blog.
Nota: equidistan significa a la misma distancia. por esto podemos decir que todos los puntos tienen la misma distancia del centro.
La sigueite es una grafica de una circunferencia.
(figura 1 representacion de una circunferencia con centro (0,0))
La circunferencia no necesariamente debe tener su centro en el origen (0,0), para otras ocasiones el centro se representa con los caracteres h = x , k = y
Procedimientos para encontrar variables
1. El Radio
para hallar el radio de una circunferencia se utilizara la distancia entre dos puntos basada en el teorema de pitagoras es decir.
Este es el conocido teorema de pitagoras para hallar la distancia entre dos puntos se utilizara la siguiente ecuacion.
Para mas informacion consulte el blog de linea recta
En esta ecucacion se utilizaran las coordenadas de un punto variable y el centro, al desarrollar la ecuacion el resultado final; la distancia sera equivalente al radio ya que la distancia del centro a un punto cualquiera de la circunferencia es igual al radio (ver explicacion anterior)
2. El Diametro
Para encontrar el diametro como ya se habia explicado antes, sera unicamente necesario doblar el radio puesto que el diametro es el radio multiplicado por dos.